Bảng công thức lượng giác trong toán học cần ghi nhớ

Giải yêu thích Giải yêu thích

Ngoại Hạng Anh

Premier League

Cúp C1 Châu Âu

Champions League

Cúp C2 Châu Âu

Europa League

VĐQG Tây Ban Nha

La Liga

VĐQG Đức

Bundesliga

VĐQG Italia

Serie A

VĐQG Pháp

Ligue 1

VĐQG Việt Nam

V-League

Thứ tư 13/04/2022 10:31:42 (GMT+7)

Công thức lượng giác là một trong số những kiến thức toán học để giải các bài toán thuộc trương trình học THPT. Vậy các công thức lượng giác cơ bản như thế nào? Để biết thêm chi tiết về vấn đề này mời bạn theo dõi bài phân tích sau đây của tyso.info.

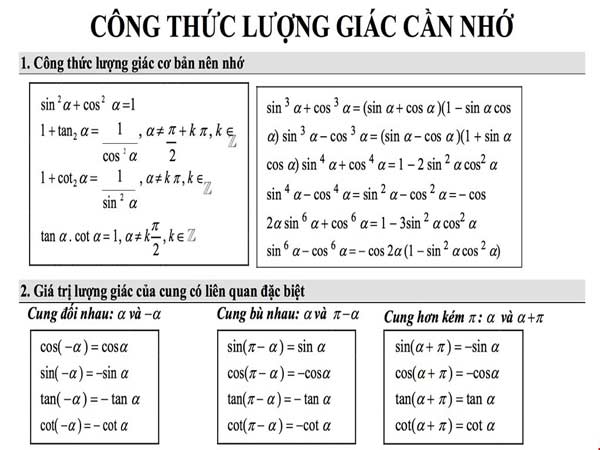
Công thức Lượng giác cơ bản

$\tan x = \frac{sinx}{cosx}$	$cotx = \frac{cosx}{sinx}$
sin²x + cos²x = 1	tan x . cot x = 1
1 + tan² x = $\frac{1}{\cos^{2}x}$	1 + cot² x = $\frac{1}{\sin ^{2}x}$

Phương pháp ghi nhớ bằng thơ dễ hiểu:

Công thức: Sin bình + cos bình = 1

Công thức: Sin bình thì bằng tan bình trên tan bình cộng 1

Công thức: Cos bình bằng một trên một cộng tan bình

Công thức: Một trên sin bình bằng 1 cộng cot bình

Công thức: Một trên cos bình bằng một cộng tan bình

Công thức: Bắt được quả tan,

Sin nằm trên cos,

Cot cải lại,

Cos nằm trên sin.

Hoặc là:

Bắt được quả tan,

Sin nằm trên cos (tan x = sin x / cos x),

Cot dại dột,

Bị cos đè cho (cot x = cos x / sin x).

Công thức Lượng giác cơ bản

Công thức cộng

cos(a + b) = cos a.cos b – sin a.sin b	cos(a – b) = cos a.cos b + sin a.sin b
sin(a + b) = sin a.cos b + sin b.cos a	sin(a – b) = sin a.cos b – sin b.cos a
tan(a + b) = $\frac{{\tan a + \tan b}}{{1 - \tan a.\tan b}}$	tan(a – b) = $\frac{{\tan a - \tan b}}{{1 + \tan a.\tan b}}$

Bài thớ ghi nhớ công thức cộng:

Công thức: Cos cộng cos thì bằng hai cos cos

Công thức: Cos trừ cos phải bằng trừ hai sin sin

Công thức: Sin cộng sin thì bằng hai sin cos

Công thức: Sin trừ sin bằng hai cos sin.

Công thức: Sin thì sin cos cos sin

Công thức: Cos thì cos cos sin sin nhớ nha dấu trừ

Công thức: Tan tổng thì lấy tổng tan

Chia một trừ với tích tan, dễ mà.

Công thức vòng tròn lượng giác

Góc đối nhau ( cos đối)	Góc bù nhau (sin bù)	Góc phụ nhau (Phụ chéo)	Góc hơn kém (Khác pi tan)
cos (-α) = cos α	sin (π – α) = sin α	sin (π/2 – α)= cos α	sin (π + α) = – sin α
sin (-α) = -sin α	cos (π – α) = – cos α	cos (π/2 – α) = sinα	cos (π + α) = – cosα
tan (-α) = – tan α	tan ( π – α) = – tan α	tan (π/2 – α) = cot α	tan (π + α) = tanα
cot (-α) = -cot α	cot (π – α) = – cot α	cot (π/2 – α) = tan α	cot (π + α) = cotα

Công thức tính cung hơn kém π / 2

cos(π/2 + x) = – sinx
sin(π/2 + x) = cosx

Bài vè ghi nhớ bảng công thức lượng giác

Cos đối, sin bù, phụ chéo, khác pi tan.

Cosin của 2 góc đối thì bằng nhau.

Sin của 2 góc bù nhau cũng bằng nhau.

Phụ chéo là 2 góc phụ nhau thì sin góc này bằng cos góc kia.

Tan góc này bằng Cot góc kia.

Tan của 2 góc hơn kém pi cũng bằng nhau.

Công thức nhân

Công thức nhân đôi

sin2a = 2sina.cosa
cos2a = cos²a – sin²a = 2cos²a – 1 = 1 – 2sin²a
tan2a = $\frac{{2\tan a}}{{1 - {{\tan }^2}a}}$

Bài vè:

Sin gấp đôi thì bằng 2 lần sin cos

Cos gấp đôi bằng bình cos trừ bình sin, bằng luôn hai cos bình trừ đi 1, cũng bằng một trừ hai sin bình mà thôi.

Tang gấp đôi, ta lấy 2 tang chia đi một trừ bình tang ra liền.

Công thức nhân ba

sin3a = 3sina – 4sin³a
cos3a = 4cos³a – 3cosa
tan3a = $\frac{{3\tan a - {{\tan }^3}a}}{{1 - 3{{\tan }^2}a}}$

Bài vè giúp ghi nhớ nhanh hơn:

Nhân 3 một góc bất kỳ.

Sin thì ba bốn, Cos thì bốn ba.

Dấu trừ đặt giữa hai ta, lập phường thì bốn chổ, thế là ra ngay.

Công thức hạ bậc

${\sin ^2}a = \frac{{1 - \cos 2a}}{2}$	${\cos ^2}a = \frac{{1 + \cos 2a}}{2}$
${\sin ^3}a = \frac{{3\sin a - \sin 3a}}{4}$	${\cos ^3}a = \frac{{3\cos a + \cos 3a}}{4}$

Công thức biến đổi tổng thành tích

$\cos a + \cos b = 2\cos \frac{{a + b}}{2}.\cos \frac{{a - b}}{2}$	$\cos a - \cos b = - 2\sin \frac{{a + b}}{2}.\sin \frac{{a - b}}{2}$
$\sin a + \sin b = 2\sin \frac{{a + b}}{2}.\cos \frac{{a - b}}{2}$	$\sin a - \sin b = 2\cos \frac{{a + b}}{2}.\sin \frac{{a - b}}{2}$

Bài vè ghi nhớ:

Sin tổng lập tổng sin cô.

Cô tổng lập hiệu đôi cô đôi chàng.

Tan tổng thì lập tổng hai tan.

Một trừ tan tích mẫu mang thương sầu.

Gặp hiệu ta chớ phải lo.

Đổi trừ thành cộng ghi sâu trong lòng.

Công thức biến đổi tích thành tổng

$\cos a.\cos b = \frac{1}{2}\left[ {\cos \left( {a + b} \right) + \cos \left( {a - b} \right)} \right]$
$\sin a.\sin b = -\frac{1}{2}\left[ {\cos \left( {a + b} \right) - \cos \left( {a - b} \right)} \right]$
$\sin a.\cos b = - \frac{1}{2}\left[ {\sin \left( {a + b} \right) + \sin \left( {a - b} \right)} \right]$

Bài vè ghi nhớ phương trình lượng giác

Cos cos thì nữa cos cộng cộng cos trừ.

Sin sin thì trừ nữa cos cộng trừ cos trừ.

Sin cos thi nữa sin cộng cộng sin trừ.

8. Nghiệm phương trình lượng giác

Phương trình cơ bản

Trường hợp đặc biệt

$\sin a = \sin b \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {a = b + k2\pi } \\ {a = \pi - b + k2\pi } \end{array}} \right.\left( {k \in \mathbb{Z}} \right)$

$\cos a = \cos b \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {a = b + k2\pi } \\ {a = - b + k2\pi } \end{array}} \right.\left( {k \in \mathbb{Z}} \right)$

$\tan a = \tan b \Leftrightarrow a = b + k\pi ;\left( {k \in \mathbb{Z}} \right)$

$\cot a = \cot b \Leftrightarrow a = b + k\pi ;\left( {k \in \mathbb{Z}} \right)$

$\sin a = 0 \Leftrightarrow a = k\pi ;\left( {k \in \mathbb{Z}} \right)$

$\sin a = 1 \Leftrightarrow a = \frac{\pi }{2} + k2\pi ;\left( {k \in \mathbb{Z}} \right)$

$\sin a = - 1 \Leftrightarrow a = - \frac{\pi }{2} + k2\pi ;\left( {k \in \mathbb{Z}} \right)$

$\cos a = 0 \Leftrightarrow a = \frac{\pi }{2} + k\pi ;\left( {k \in \mathbb{Z}} \right)$

$\cos a = 1 \Leftrightarrow a = k2\pi ;\left( {k \in \mathbb{Z}} \right)$

$\cos a = - 1 \Leftrightarrow a = \pi + k2\pi ;\left( {k \in \mathbb{Z}} \right)$

Bảng dấu của các giá trị lượng giác

Góc phần tư số	I	II	III	IV
Giá trị lượng giác	I	II	III	IV
sin x	+	+	–	–
cos x	+	–	–	+
tan x	+	–	+	–
cot x	+	–	+	–

Xem thêm: 1 hải lý bằng bao nhiêu m? Công thức chuyển đổi cơ bản

Một số công thức lượng giác bổ sung

$\sin a + \cos b = \sqrt 2 \sin \left( {\alpha + \frac{\pi }{4}} \right) = \sqrt 2 \cos \left( {\alpha - \frac{\pi }{4}} \right)$
$\sin a - \cos b = \sqrt 2 \sin \left( {\alpha - \frac{\pi }{4}} \right) = - \sqrt 2 \cos \left( {\alpha + \frac{\pi }{4}} \right)$
tan a + cot a = $\frac{2}{{\sin 2a}}$
cot a – tan a = 2cot 2a
sin⁴a + cos⁴a = 1 – $\frac{1}{2}$ sin²2a = $\frac{1}{4}$ cos4a + $\frac{3}{4}$
sin⁶a + cos⁶a = 1 – $\frac{3}{4}$ sin²2a = $\frac{3}{8}$ cos4a + $\frac{5}{8}$

Biểu diễn công thức theo $t = \tan \frac{\alpha }{2}$

$\sin \alpha = \frac{{2t}}{{1 + {t^2}}}$
$\cos \alpha = \frac{{1 - {t^2}}}{{1 + {t^2}}}$

$\tan \alpha = \frac{{2t}}{{1 - {t^2}}}$
$\cot \alpha = \frac{{1 - {t^2}}}{{2t}}$

Trên đây là một số thông tin liên quan đến việc tìm hiểu bảng công thức lượng giác cơ bản. Hy vọng những thông tin kiến thức mà chúng tôi chia sẻ đã giúp bạn hiểu rõ hơn về vấn đề này.