Tìm hiểu công thức hạ bậc trong bằng công thức lượng giác
(GMT+7)
Trong bảng công thức lượng giác thì công thức hạ bậc được xem là một công thức vô cùng quan trọng khi giải các bài tập lượng giác. Vậy các dạng bài tập của công thức này như thế nào? Để biết thêm chi tiết về vấn đề này mời bạn theo dõi bài phân tích sau đây của tyso.info.
Công thức hạ bậc lượng giác
Lượng giác là gì?
Lượng giác trong tiếp anh có tên là Trigonometry. Đây là một kiến thức toán học được áp dụng trong chương trình học phổ thông của Việt Nam.Việc nghiên cứu lượng giác để tìm hiểu hình tam giác và sự liên kết giữa cạnh của hình tam giác cũng với những góc độ khác của nó. Lượng giác là sự thể hiện bên ngoài của các hàm số lượng giác, mà hàm số lượng giác chính là sự thể hiện các mối liên hệ bên trong của tam giác và có thể áp dụng được để học các hiện tượng có chu kỳ như song âm.
Hạ bậc lượng giác là gì?
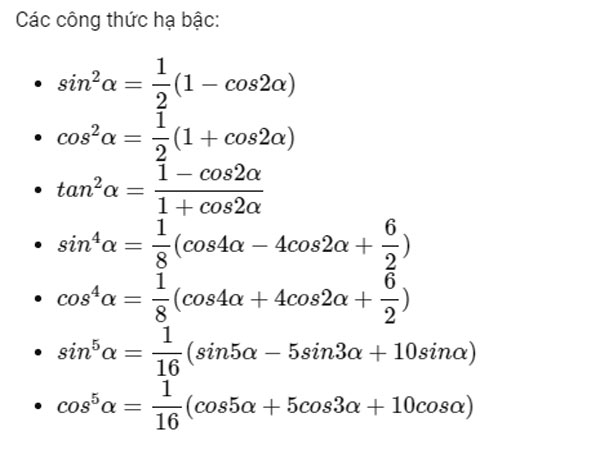
Công thức hạ bậc lượng giác là một công thức được áp dụng để đưa các hàm số lượng giác có bậc cao về bậc thấp hơn nó. Từ đó tạo điều kiện giải phương trình lượng giác được đơn giản và dễ hiểu hơn. Cụ thể công thức hạ bậc trong bằng công thức lượng giác được áp dụng như sau:
Để ghi nhớ được công thức hạ bậc được nhanh và hiệu quả thì bạn nêm nắm chắc dạng bài và làm bài tập thường xuyên. Ngoài ra bạn có thể trao đổi thêm với bạn bè về cách áp dụng công thức hạ bậc trong giải các phương trình lượng giác như vậy cũng giúp bạn hiểu rõ được bài tập mà bạn đang làm.
Ngoài ra công thức hạ bậc chỉ là một bước nhỏ trong cách giải phương trình lượng giác nhưng nó có thể xem là một bước suy ra quan trọng giúp bạn giải toán được nhanh và hiệu quả hơn so với việc để hàm số có bậc quá cao. Trong quá trình hạ bậc nên lưu ý về điều kiện để thực hiện hạ bậc. Bởi vì có một số bài toán nếu không đủ điều kiện thì bạn sẽ không thực hiện hạ bậc được.
Một số bài tập áp dụng CT hạ bậc cơ bản
Bài tập 1. Thực hiện giải PT lương giác sau: sin3a + cos3a = 0
Lời giải
(1 – cos3a)/2 + cos3a = 0
⇔1 – cos3a + 2cos3a = 0
⇔1 + cos3a = 0
⇔ cos3a = -1
⇔3a = π + k2π
Vậy nghiệm của phương trình lượng giác này là 3a = π + k2π
Bài tập 2: Hãy giải phương trình sin2x = cos2x + cos25x
Lời giải
Biến đổi phương trình về dạng:
(1 – cos2x)/2 = (1 + cos4x)/2 + cos25x
⇔ 2cos25x + (cos4x + cos2x) = 0
⇔ 2cos25x + 2cos3x.cos5x = 0
⇔ (cos3x + cosx) cos5x = 0
⇔ 2cos2x.cosx.cos5x = 0
Xem thêm: Tìm hiểu công thức sin cos lượng giác cơ bản nhất
Trên đây là một số thông tin liên quan đến việc tìm hiểu công thức hạ bậc và một số dạng bài tập áp dụng công thưucs hạ bậc đơn giản. Hy vọng những thông tin mà chúng tôi chia sẻ đã giúp bạn hiểu rõ hơn về vấn đề này.






